Mit der Frequenz-Antwortanalyse (FRA – frequency responce analysis) kann gezielt die Höhe der Anregung in Form von Kraft oder Beschleunigung auf eine beliebige Struktur gegeben werden. Auch die Richtung der Anregung kann hinterlegt werden.

Während bei der Modalanalyse eine normierte Anregung in allen Raumrichtungen aufgeprägt wurde um die Eigenmoden zu ermitteln, kann bei der FRA gezielt eine Belastungsrichtung ausgewählt und die Höhe angegeben werden.

Mit der Modalanalyse lassen sich Bauteile oder auch Baugruppe auf Eigenfrequenzen analysieren. Dabei wird im Prinzip die geometrische Struktur mit allen möglichen Frequenzen angeregt und dabei ermittelt, bei welchen Frequenzen Bauteilschwingungen über ein zulässiges Maß entstehen.

Eigenfrequenzen sind diejenigen Frequenzen, bei denen sich Strukturen oder Bauteile von selber in der Schwingungsamplitude aufschwingen. Dabei entstehen sehr hohe Bauteilbelastungen die bis zum Bruch der Bauteile führen können. Im weniger schlimmen Fall wirken sich die Schwingungen auf die Geräuschentstehung oder in Form von spürbaren und unangenehmen Vibrationen aus.

Mit Pro/Mechanica können lineare Schwingungssysteme analysiert werden. Dazu wird ein Simulationsmodell aufgebaut. Das Modell ist dasselbe wie bei der Modal-Analyse mit einem Unterschied: das Anregungsspektrum muss an einem bestimmten Punkt in eine bestimmte Richtung eingebracht werden. Um die Resonanzanwort zu erhalten, müssen an verschiedenen auszuwertenden Punkten Messgrößen gesetzt werden, an denen dann Ergebnisse ausgewertet werden können.

Starre Verbindungen/Kopplungen einsetzen

Aufgrund der Einschränkung auf ein lineares Schwingungssystem sind nur starre Kopplungen von Körpern möglich (Verkleben bzw. Verschweißen). Kontaktdefinitionen jeglicher Art sind hierbei nicht möglich, da dies bereits einen nichtlinearen Kontakt darstellen würde.

Einspannungen definieren

Zusätzliche Masse einbringen

Einbringen von zusätzlicher Masse an bestimmten Punkten. Diese kann andere Bauteilmassen simulieren, welche letztlich auf ihre Masse und ihren Schwerpunkt und ihren Trägheitstensor reduziert werden können. In diesem Falle ist es noch einfacher, es soll lediglich die Hälfte der Masse der Schaltmuffe mit simuliert werden.

Letztlich muss wie immer bei Pro/Mechanica für jedes Bauteil die Dichte, die Querkontraktionszahl und die richtigen Einheiten hinterlegt werden.

Die Höhe der Spannungen oder der Verschiebung kann nur dann quantitativ ausgewertet, wenn die Anregung in der Richtung und Höhe bekannt ist und vorgegeben wird. Dies kann nur mittels FRA durchgeführt werden. Es kann eine Dämpfung hinterlegt werden, welche meistens zwischen 0,5 und 1 angenommen wird. Genauere Dämpfungswerte können nur aus Messungen mittels Dehnmessstreifen (DMS) ermittelt werden um diese dann bei weiteren Simulationen hinterlegen zu können.

Amplitude und Richtung der Kraft an definierter Stelle einbringen

Im vorliegenden Fall des Schaltsystems soll für den (Fehler-) Fall des Schaltratschens eine überhöhte Kraft auf die Schaltpatte gegeben werden, die in Bewegungsrichtung der Schaltmuffe gerichtet ist. Kommt es zum (fehlerhaften) Fall, dass die Sperrsynchronisierung einen zu geringen Sperrwert aufweist, kann der Formschluss zwischen Schaltmuffe und Kupplungskörper noch bei Differenzdrehzahl versucht werden herzustellen. Dies äußert sich dahingehend, dass die Zahnspitzen aneinander reiben und es zu keinem Formschluss kommen kann, wohl aber zu einem Aufschwingen des Systems in axialer Schaltrichtung. Die daraus entstehende Kraft wird als Erfahrungswert als Eingangsgröße für das Schaltsystem genommen.

Unter dieser Betrachtung wurden die Schaltelemente statisch bereits berechnet und dürfen sich dabei nicht plastisch verformen. Eine statische Analyse stellt im Rahmen der Schwingungsanalyse den Sonderfall Frequenz f=0 Hz dar. Auch bei anderen Frequenzen die weit weg genug von der Resonanz sind wird diese Betrachtung weiterhin stimmen. Aber direkt bei Anregung nahe der Resonanzfrequenzen kommt es zu deutlich höheren Bauteilbelastungen, die zu plastischen Verformungen oder auch zum Bruch des Bauteils führen kann.

Hintergründe und Theorie zur Frequenzanalyse

Allgemeine Schwingungen im Zeitbereich haben eine Amplitude und eine Frequenz. Ein Signal mit einer Sinusschwingung beispielsweise hat nur eine einzige Frequenz und eine Amplitude. In der Realität sind fast immer verschiedene Frequenzen überlagert, wodurch es schwierig ist, diese Schwingungen voneinander zu trennen.

Eine Möglichkeit hierfür ist die Fourier-Transformation des zeitkontinuierlichen Signals (x-Achse ist die Zeitachse, y-Achse die Amplidude) in den Frequenzbereich (Spektralanalyse). Stellt man dann das Signal fouriertransformiert dar, so ist auf der x-Achse die Frequenz abgetragen und auf der Y-Achse weiterhin die Amplitude. Das Verfahren versucht zu jeder Schwingung die überlagerten Einzelschwingungen zu finden und diese dann darzustellen. Das gelingt umso besser, je höher die Energieanteile bzw. Amplituden der Einzelschwingungen sind. Sind viele Schwingungen mit ähnlicher Frequenz vorhanden, wird keine klare Frequenz ermittelt, sondern ein Frequenzband.

Zitat von Wolfgang Wokurek, 2001:

„Die Stärke eines Signals wird auch als Amplitude des Signals (Signalamplitude) bezeichnet. Das gilt für die Amplituden des zeitkontinuierlichen (auch analogen) Signals x(t) wie für dessen Abtastwerte, die Amplituden des zeitdiskreten Signals x(n). Aus diesen linearen Amplituden des Signals werden wichtige quadratische Größen berechnet. Das ist zunächst die Momentanleistung des zeitdiskreten Signals, die aus den quadrierten Amplituden x2(n) besteht. Linear oder quadratisch bezeichnet hier die Abhängigkeit der Größe von Veränderungen der Signalstärke. So bewirkt die Verdoppelung der Signalstärke die Verdopplung der linear abhängigen Größen die Vervierfachung der quadratischen Größen. Umgekehrt halbieren sich linear abhängige Größen bei halber Signalstärke und quadratisch abhängige Größen werden geviertelt. Die Summe aller Momentanleistungen ∑x2(n) ist die Energie des zeitdiskreten Signals ebenfalls eine quadratische Größe. Bei Signalen unendlicher Dauer -∞<n<+∞ muss die Existenz dieser Summe erst noch überprüft werden. Hier werden Signale endlicher Dauer und endlicher Amplitude vorausgesetzt.

Die Wörter Leistung und Energie werden in der Signalverarbeitung nicht immer im korrekten physikalischen Sinn verwendet. Dort sind meist mehrere verschiedene Messgrößen zur Berechnung der Leistung und Energie erforderlich (z.B. Spnnung und Strom, Schalldruck und Schallschnelle). In der Signalverarbeitung ist das wesentliche Unterscheidungsmerkmal zwischen Amplitude und Leistung die Art der Abhängigkeit bei Signalskalierung (z.B. Halbierung, Verdopplung), nämlich linear wie Amplitude, RMS, Effektivwert oder quadratisch wie Leistung, mittlere Leistung, Energie, Kurzzeitenergie.

Ein anderes Unterscheidungsmerkmal ist die Frage nach der Zeitnormierung: wie verhält sich doe Größe, wenn das betrachtete Zeitintervall verlängert oder verkürzt wird. Die mittlere Leistung ist (bei einem stationären Signal) unabhängig von dieser Intervalldauer. Quadratisch von der Intervalldauer abhängige Größen sind sogenannte Wirkungen <Energie x Zeit>.

Effektivwert  - RMS (root of mean of squares)

Der RMS-Wert eines Signalstücks ist jene konstante Signalamplitude, welcher die selbe mittlere Leistung wie dem Signalverlauf zugeordnet ist. In der Signal- und Systemtheorie wird die Signalleistung px(n) eines zeitdiskreten, reellwertigen Signals x(n) durch

px(n) = x2(n)

definiert. Die Signalleistung px(n) ist eine nicht negative Größe:

px(n) ≥ 0;

sie verschwindet genau dann, wenn auch das Signal x(n) verschwindet. Die Summe aller Signalleistungswerte px(n) ergibt die Energie des Signals

Ex = ∑ px(n)

Auch die Signalenergie nimmt keine negativen Zahlenwerte an: Ex ≥ 0. Sie verschwindet nur dann, wenn alle Signalwerte verschwinden. Wird nicht die Gesamtenergie eines Signalelements sondern nur die Energie des Segments [a,b], d.h. für x(n), a ≤ n ≤ b, dann ist das die Kurzzeitenergie:

Ex;a,b = ∑ px(n)

Aus der Kurzzeitenergie eines Signalelements lässt sich die mittlere Leistung des Signalsegments berechnen:

pquer;a,b = Ex;a,b / Na,b

Dabei wird die Kurzzeitenergie Ex;a,b  durch die Anzahl der Abtastwerte Na,b  = b - a + 1 des Segments [a,b] geteilt. Der Effektivwert oder RMS ist schließlich jene Amplitude, welche als Konstante im Segment [a,b] diesselbe Kurzzeitenergie hätte wie das Signal.

Daraus folgt der Effektivwert oder RMS zu

Dieser Wert wird zwar aus der mittleren Leistung berechnet, hat wegen der Quadratwurzel aber wieder die Dimension einer Signalamplitude. Die Bezeichnung RMS gibt übrigens den Berechnungsvorgang wieder. Zunächst werden die Signalamplituden quadriert, deren Mittelwert wird berechnet und dessen Quadratwurzel ist der Effektivwert.

RMS ≭ Standardabweichung

Dem Effektivwert und der Standardabweichung einer Stichprobe liegen verschiedene Konzepte zugrunde. Auch die Berechnungsformeln sind verschieden. Die Standardabweichung 𝜎x ist als Quadratwurzel des Erwartungswert E der quadrierten Abweichungen einer Zufallsvariable x von deren Mittelwert μx definiert.

Mittelwert und Standardabweichung sind also für Zufallsvariablen definiert. Dagegen ist der Effektivwert (RMS) eine (fiktive) Signalamplitude. Dies ist ein konzeptioneller Unterschied.

Die Standardabweichung beschreibt die Abweichung vom Mittelwert. Der Effektivwert (RMS) beschreibt die Signalabweichung vom Nullpunkt. Dieser Unterschied wird am kleinsten bei mittelwertfreien Signalen (μx=0).

Doch selbst bei mittelwertfreien Signalen (bzw. Stichproben) hat der Schätzer der Standardabweichung 𝜎x eine andere Gestalt:

Die quadrierten Abweichungen werden also nicht gemittelt, sondern es wird durch N-1 geteilt. Dieser formale Unterschied ist numerisch am größten bei kurzen Signalen (d.h, kleinen Stichproben).

Leistungsverhältnisse (Bel, Dezibel)

Das Größenverhältnis zweier Leistungswerte (allgemeiner auf quadrierten Signalwerte bezogene Größen wie Energie, Kurzzeitenergie, Effektivwert, Schallintensität) L1 und L2 wird durch Division

berechnet. Sind die beiden Leistungen von sehr verschiedener Größenordnung, dann ergibt das Verhältnis sehr große (oder sehr kleine), oft unhandliche Zahlenwerte. Z.B. stehen die Schallintensitäten der Schmerzgrenze

und der Ruhehörschwelle

im Verhältnis

Um diese unhandlichen Zahlenwerte für leistungsartige Verhältnisse übersichtlicher darzustellen wird ein logarithmischer Maßstab verwendet

Dieses logarithmische Verhältnis bekam den Namen „Bel“ (nach dem Erfinder des Telefon Alexander Graham Bell (1847-1922)). Dabei wird der dekadische Logarithmus verwendet, das Intensitätsverhältnis zwischen der Schmerzgrenze und der Ruhehörschwelle ist in diesem Maßstab also

Der Rechenregel für Logarithmen entsprechend ist der Logarithmus des Verhältnisses gleich der Differenz der Logarithmen des Zählers und des Nenners

also z.B.

Dieser logarithmische Bel-Maßstab ist für viele Anwendungen zu grob, d.h. die relevanten Unterschiede zwischen Bei-Werten treten oft erst in den Nachkommastellen auf. Daher ist die Verwendung eines zehnfach vergrößerten Maßstabs üblich. Diese Untereinheit des Bel heißt Dezibel (abgekürzt dB, Dezi als Vorsilbe für 0,1 = 10-1). Das Intensitätsverhältnis zwischen der Schmerzgrenze und der Ruhehörschwelle beträgt dann:

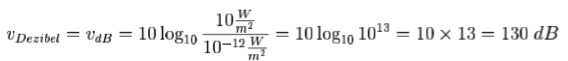
Ist eine der beiden Leistungen L1 oder L2 und das Leistungsverhältnis in Dezibel vdB bekannt, dann kann die andere Leistung nach

berechnet werden. Die Rückrechnungsformel für Leistungsverhältnisse in Bel vB sind

Bezugsleistung

Oft werden einzelne Messgrößen in dB angegeben. Steht diese Tatsache nicht im Widerspruch zur Behauptung, dass Dezibel immer ein logarithmisches Leistungsverhältnis darstellt?

Oft werden zunächst Leistungsmesswerte gesammelt, die erst später, bei der Auswertung, zueinander ins Verhältnis zu setzen sind. Da oft gleich eine Angabe in Dezibel gewünscht wird, kann dies unter Verwendung einer festen Bezugsleistung geschehen. Die Wahl der Bezugsleistung ist beliebig, sofern alle Umrechnungen mit derselben Größe erfolgen. Da die Wahl der Bezugsleistung beliebig ist, kann ein Wert gewählt werden, der die Berechnung vereinfacht. Wird z.B. die Bezugsleistung L2=1 verwendet, dann vereinfacht sich die Umrechnungsformel zu

Wenn die Bezugsgröße nicht aus dem Zusammenhang klar ist, dann wird diese als zusätzlicher Index notiert (vdB,1). Die Bezugsleistung 1 wird oft stillschweigend von Signalverarbeitungsprogrammen bei der Umrechnung von Amplituden oder Leistungen in Dezibel verwendet.

Zwei mit der selben Bezugsgröße in Dezibel verwandelte Leistungen a und b lassen sich durch Subtraktion dieser Dezibelwerte adB,L0, bdB,L0 ins Verhältnis setzen

Dabei bedeutet L0 die Bezugsleistung und die Rechnung liegt, dass ihre Größe keinen Einfluss auf das Ergebnis adB,L0- bdB,L0 hat.

Bei der Schallpegelmessung liegt ein ähnlicher Fall vor. Dort interessieren sehr oft nur Schallpegel, die für Menschen wahrnehmbar sind. In diesen Fällen bietet sich die Ruhehörschwelle des Menschen als Bezugspegel ab. Dieser Liegt nahe bei 1012 W/m2, der als Bezugsintensität für Schallpegelmessung in Dezibel verwendet wird.

Amplitude oder RMS in dB?

Der RMS-Wert eines Signalsegments heißt auch Effektivwert und ist jene konstanten Signalamplitude, welche die selbe Energie wie das Signal hat. Ist die Umrechnung von Amplitudenwerten wie des RMS in dB nicht ein Widerspruch zur Definition von Dezibel als logarithmisches Maß für Leistungen?

Im strengen physikalischen Sinn stimmt dieser Einwand. Da in der Signalverarbeitung jedoch Leistungen durch einfaches Quadrieren von Amplitudenwerten, insbesondere ohne Notwendigkeit zur Einbeziehung weiterer Signale berechenbar sind, wird dieser Zwischenschritt des Quadrieren von Amplitudenwerten einfach in die Rechnung einbezogen. Sind also die Amplituden A1 und A2 gegeben, dann sind die zugehörigen Leistungen L1 = A12 und L2 =A22. Das Leistungsverhältnis in Bel beträgt dann

und in Dezibel

Zur Berechnung einer Amplitude aus der anderen Amplitude und dem Leistungsverhältnisse in Bel vb gelten

Liegt das Leistungsverhältnis in Dezibel vdB vor, gelten

Ergebnisse der Berechnung

Die Ergebnisse einer frequenzabhängigen Simulation mit gegebener Lasthöhe und Lastrichtung können sein:

1. • Spannungen (v.Mises, max. Hauptspannungen u.a.)
   

2. • Verschiebungen in mm
   

3. • Dehnungen in %
   

4. • Beschleunigung usw.
   

Für jede angeregte Frequzenz kann man sich jetzt die Anwort getrennt anzeigen lassen. Schnell wird sichtbar, wie die max. Verschiebung an jeder gewünschten Stelle aussieht.

Interessanter als die max. Verschiebung sind die max. Spannungen.

Problematisch wird es immer dann, wenn für einen Lastfall eine Spannung oberhalb der Streckgrenze entsteht. Wird der Spannungsbereich zwischen Streckgrenze und Bruchspannung nur kurzzeitig erreicht, kann das Bauteil das zeitfest vielleicht noch aushalten, wenn auch mit plastischen Verformungen.

Stellt man den Bereich beispielsweise eines Alubauteils oberhalb der Rp0,2-Grenze als rot dar, dann dürfte dieses Bauteil deutlich überlastet sein und würde sehr schnell plastisch verformen und brechen. Gerade Alu neigt zum Sprödbruch wenn mehrfach im plastischen Bereich verformt und zurückverformt wird.

Aber auch die Verschiebungen in mm sind bei der Auswertung sichtbar. Dadurch läßt sich die Schwingungsamplitude an allen möglich Stellen darstellen und eine hohe Auslenkung kann bewertet werden.

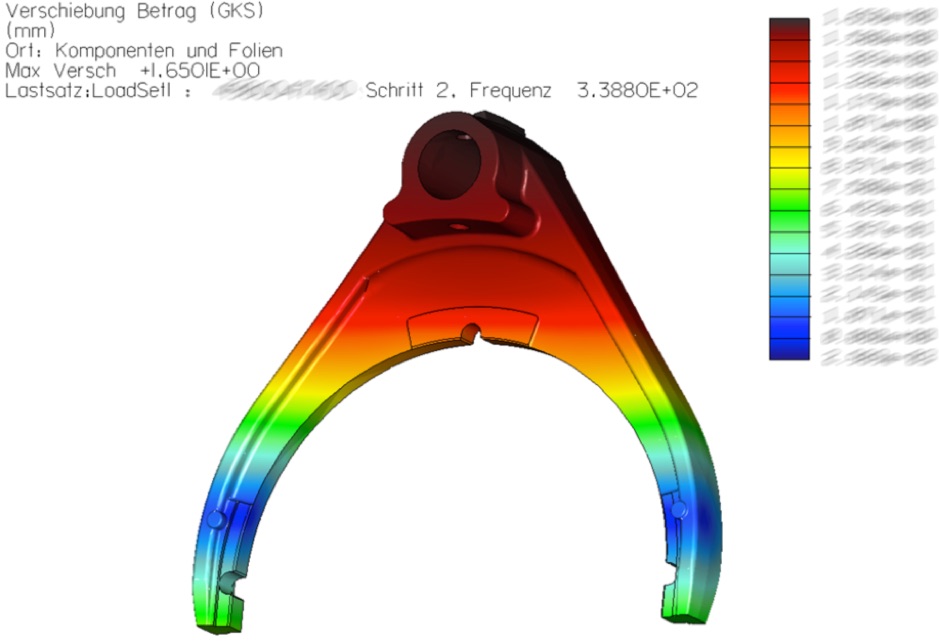
Einschränkend läßt sich sagen, dass bislang rein linear elastisch gerechnet wurde, also ohne Dämpfung im Werkstoff. Würde diese ebenfalls noch berücksichttigt, so reduziert sich die Amplitude etwas. Die Dämpfung lässt sich ebenfalls in Pro/Mechanica eintragen und damit mit berücksichtigen.