Bei der Untersuchung von Messsignalen hinsichtlich darauf enthaltener Frequenzen oder Motorordnungen können verschiedene Signalquellen enthalten sein. Liegt ein Messsignal beispielsweise eines Beschleunigungsmessaufnehmers vor, dann werden darin zahlreiche Signale enthalten sein. Ziel der Frequenzanalyse ist es jetzt, diese Signale zu erkennen und zu bekannten Ursachen zuzuweisen.

Eine solche Quelle kann ein sogenanntes pulsweiten-modelliertes Signal (PWM) sein. Dabei handelt es sich um eine in der elektrischen Welt üblichen Daten- und Energieübertragungsweise, die mittels schnell schaltenden Halbleitern umgesetzt werden kann. Immer wenn Ströme geregelt, begrenzt oder gestellt werden müssen, wird auf dieses Verfahren zurückgegriffen.

Was ist PWM? Hier nur eine kurze Einleitung:

1. • es soll ein Strom (z.B. 5 Ampere) geschaltet werden, womit eine elektrische Spule bestromt wird und damit ein vom Strom abhängig starkes Magnetfeld erzeugt wird. Damit soll etwas angetrieben oder eine Kraft erzeugt werden.
   

2. • es soll genau dieser Strom gestellt werden ... sehr kurze Zeit 0,05s später 6 A und nach nochmals 0,05s nur noch 4 Ampere
   

3. • es steht auf Erzeugerseite eine bestimmte Spannung zur Verfügung, die konstant ist. Da Strom gleich Spannung durch Widerstand ist (U=RxI) muss für einen bestimmten Strom exakt ein bestimmter Wiederstand bereitgestellt werden.
   

4. • mittels schnell schaltender Halbleiter kann ein Widerstand in kurzen Zeitintervallen bestromt werden und damit ein immer gleich hoher Strom erzeugt werden. Die Höhe ist nicht beeinflussbar, nur die Zeitdauer wie lange dieser bereitgestellt wird. Wird der Halbleiter z.B. mit einer bestimmten Taktfrequenz geschaltet, so können damit das Verhältnis der bestromten Zeit und der nicht bestromten Zeit beeinflusst werden.
   

5. • in Verbindung mit Induktivitäten und Impedanzen (frequenzabhängigen Widerständen) kann so ein zeitlich gemittelter Strom erzeugt werden. Eine dynamische Stromquelle kann einen verhältnismäßig trägen Strom in der Spule ändern.
   

6. • Die gemittelte Stromhöhe kann über das Tastverhältnis (Verhältnis der Strom-An-Zeit zur Periodendauer) - angegeben in Prozent - eingestellt werden. Ein Tastverhältnis von 100% entspricht dabei einem konstantem Strom-An-Signal, ein Tastverhältnis von 50% gleich langen Anteilen von Stron-An und Strom-Aus.
   

Im Folgenden sehen wir als Signal ein solches PWM-Signal über der Zeit. Darunter ist das mittels Fast-Fourier-Transformation (FFT) zerlegte Signal mit seinen Frequenzbestandteilen zu sehen.

Beim ersten Beispiel möchten wir eine PWM-Frequenz von 50 Hz betrachten, das Tastverhältnis dabei beträgt 50%. Dieses Signal wird im Frequenzraum mit folgenden Frequenzen dargestellt

1. • f1=0 Hz: hierüber wird der zeitliche Mittelwert angezeigt
   

2. • f2=50 Hz: die PWM-Trägerfrequenz ist immer die tiefste Frequenz (die nicht 0 ist)
   

3. • f3-f10 Hz: es werden die Harmonischen (Vielfache) von f2 dargestellt, deren Amplitude mit höheren Ordnungen immer weiter abnimmt.
   

Im zweiten Beispiel haben wir die PWM-Frequenz auf 20 Hz mit einem Tastverhältnis von 40% eingestellt. Bei der Analyse sieht man wiederum die 0 Hz und dann die 20 Hz und deren ganzzahligen Vielfache.

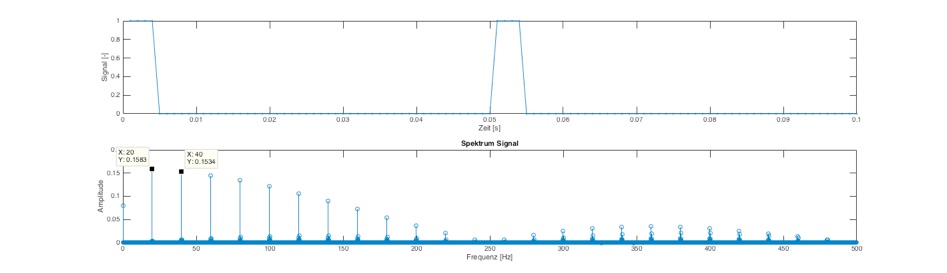
Im dritten Beispiel bleiben wir bei 20 Hz PWM-Frequenz und veringern nur das Tastverhältnis auf 10%. Damit wird die Kurve stark assymetrisch und der Anteil der höheren Ordnungen wird stärker. Aber die niedrigste Frequenz ist neben 0 Hz wieder die 20 Hz Grundfrequez.

Hier der Matlab-Code:

pwm_frequenz=10; %Hz

tastverhaeltnis = 0.5;

amplitude=1;

zeitspanne=1; %Sekunde

signal=0;

zeit=0;

schrittweite=1/pwm_frequenz/100;

zaehler=1;

for i=1:1:100001

    if (zaehler<20) %Spannung ein

        signal(i)=amplitude;

    else

        signal(i)=0; %Spannung aus

    end

    zaehler=zaehler+1;

    zeit(i)=schrittweite*i;

    if (zaehler>50)

        zaehler=1;

    end

end

Ts = diff(zeit(5:6));

Fs= 1/Ts;

N1 = length(signal);

f1=[0:floor((N1-1)/2)] / (N1*Ts);

X1= fft(signal);

X1= X1 / N1;

X1 = [X1(1) 2*X1(2:floor((N1-1)/2)+1)];

figure(1);

subplot(2,1,1);

plot(zeit, signal, '.-')

xlabel('Zeit [s]')

ylabel ('Signal [-]')

%ylim([0.5 0.638])

xlim([0 0.1])

subplot(2,1,2);

stem(f1, abs(X1))

xlabel ('Frequenz [Hz]')

%xlim([00 1000])

ylabel ('Amplitude')

%ylim([0 5000])

title ('Spektrum Signal')

Ergebnis:

Wenn wir wissen dass ein PWM-Signal vorliegen könnte, sollten wir zuerst die PWM-Frequenz herausfinden. Diese Frequenz sollte ausreichend hoch sein, damit wir nicht die vielen harmonischen Oberfrequenzen mit in unserem Frequenzbereich haben, die wir auf andere Signale untersuchen möchten. Falls das nicht umgänglich ist bleibt nur die Lösung, diese Harmonischen mittels Schmalbandfiltern herauszufiltern. Diese sind dann nicht mehr enthalten, aber es kann natürlich sein, dass andere Signale ebenfalls auf einer dieser sehr vielen Harmonischen liegt und damit unentdeckt bleiben.