Nicht nur in Simulink können Simulationen vorgenommen werden, auch geeignete Matlab-Routinen können hier helfen.

Möchten wir beispielsweise ein Kennfeld wie das obige Muscheldiagramm eines Verbrennungsmotors in Matlab abbilden mit dem Ziel, dass wir Drehzahl und den effektiven Mitteldruck angeben, und den spezifischen Kraftstoffverbrauch als Ergebnis bekommen, so gibt es unterschiedliche Befehle, die dies ermöglichen:

1. • 2D-Kennfelder (z.B. Wandlerkennlinie) --> interp1(n_verh_kennlinie, M_uberh_kennlinie, 0.44)
   

2. • 3D-Kennfelder --> interp2(X,Y,Z X1, X2)
   

 

1. • 4D-Kennfelder --> interp3()
   

 

1. • xD-Kennfelder --> interpn()
   

Als 2D-Kennfelder kann man all jene Kennfelder betrachten, die einem Eingangswert genau einen Ausgangswert zugeordnet haben. Dies trifft beispielsweise bei Wandlerkannfeldern, bei dem auf der x-Achse das Drehzahlverhältnis und auf der y-Achse das Momentenverhältnis oder der Wirkungsgrad abgetragen ist.

Als 3D-Kennfelder kann man das oben im Bild abgebildete Motordiagramm mit 2 Achsen als Eingangsgröße (Motordrehzahl und spez. Mitteldruck/Drehmoment) und der spez. Kraftstoffverbrauch als Funktionswert bezeichnen. Im Prinzip könnte bei einer 3D-Darstellung die muschelförmigen Verbrauchsgrößen auch auf der z-Achse nach oben in Form eines Gebirges dargestellt werden.

Als 4D-Kennfelder kann man beispielsweise das Motorkennfeld eines Elektromotors darstellen. 3 Eingangsgrößen (Spannung, Strom und Drehzahl) bestimmen den Wirkungsgrad als 4. Größe.

Wirkungsgrad eines 4-poligen 11 kW Asynchronmotors bei unterschiedlichen Drehzahlen und Belastungen

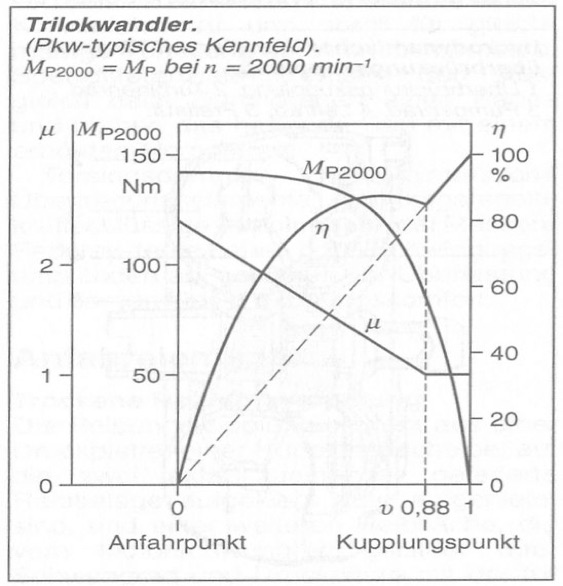
Hier eine Beispielprogrammierung für ein Wandler-Kennfeld (Drehmomentwandler):

%Randbedingungen

n3_max=20000;

k3_status='offen';

i_stufe_0_1=2;

M_antrieb_max_zug=500;

M_antrieb_max_schub=400;

wandler_M_max_zug=M_antrieb_max_zug/i_stufe_0_1;

J_SW=0.2;

% Wandlerkennlinie

n_verh_kennlinie =   [0   0.1   0.2   0.3   0.4   0.5   0.6   0.7   0.8   0.9   1    1.1   1.2   1000  10000000];

M_ueberh_kennlinie =  [1.6 1.53  1.46  1.4   1.33  1.26  1.2   1.13  1.06  1     0    0.8   0.8   0.8   0.8];

%Betriebspunkt im Wandler

n_verh=n_turbine/n_pumpe;

M_ueberh=interp1(n_verh_kennlinie, M_ueberh_kennlinie, n_verh);

M_Turbine=M_ueberh*M_Pumpe;

Kurz zum Programmaufbau:

Im ersten Abschnitt stehen die festen Parameter.

Im zweiten Abschnitt werden einige Punkte im Kennfeld angegeben, hier ein 2D-Kennfeld. Wichtig dabei ist, dass man weiß dass der erste Wert der ersten Wertereihe mit dem ersten Wert der zweiten Wertereihe zusammengehören. Bei praktisch linearen Bereichen im Kennfeld kann der Punkteabstand zueinander größer sein, als in nicht linearen. Denn alle Zwischenpunkte werden im einfachsten Fall linear interpoliert. Ändert sich ein Wert über weite Strecken nicht mehr (ist quasi konstant), dann reicht es auch hier mit großen Abständen Punkte anzugeben.

Im dritten Abschnitt wird das Kennfeld interpoliert. Zuerst muss die Eingangsgröße (der aktuelle Wert der x-Achse) errechnet werden. Dann wird der Interpolationsbefehl mit der Eingangsgröße aufgerufen und ein geeigneter Ausgabewert interpoliert. Es kann dabei nicht nur linear, sondern auch komplexer interpoliert werden, beispielsweise mit höheren Potenzen.

Details zu den entsprechenden Befehlen und Funktionen für 2D-Kennfelder (Kennlinien)

vq = interp1(x,x,xq)

Mit dieser Funktion lassen sich 2 Wertereihen x und y mittels einer linearen Interpolation aufnehmen und anschließend beliebige Zwischenwerte ausgeben. Da hierbei mit den Wertereihen eine Art Polygonzu entsteht, ist diese Art der Interpolation sehr unpräzise. Hier ein Beispielskript zum Verdeutlichen:

x = 0:pi/4:2*pi;

v = sin(x);

xq = 0:pi/16:2*pi;

figure

vq1 = interp1(x,v,xq);

plot(x,v,'o',xq,vq1,':.');

xlim([0 2*pi]);

title('(Default) Linear Interpolation');

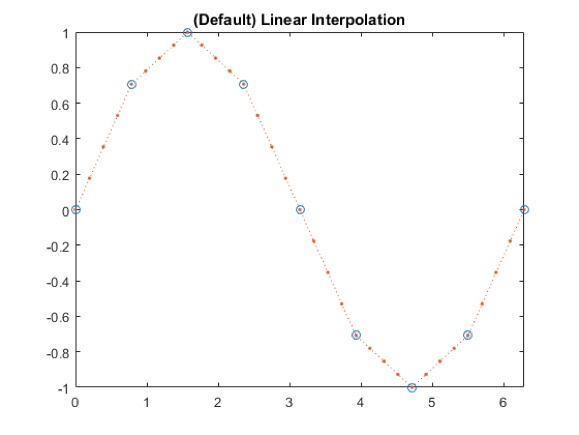
Mit einer Spline-Interpolytion werden die Zwischenwerte schon genauer. Allerdings kann es sein, dass die Charakteristik der Ursprungsfunktion (in diesem Falle der Sinus) gar nicht bekannt ist bzw. eine unbekannte Charakteristik aufweist. In diesem Fall weicht auch die Spline-Interpolation einen Fehler unbekannter Größe auf.

figure

vq2 = interp1(x,v,xq,'spline');

plot(x,v,'o',xq,vq2,':.');

xlim([0 2*pi]);

title('Spline Interpolation');

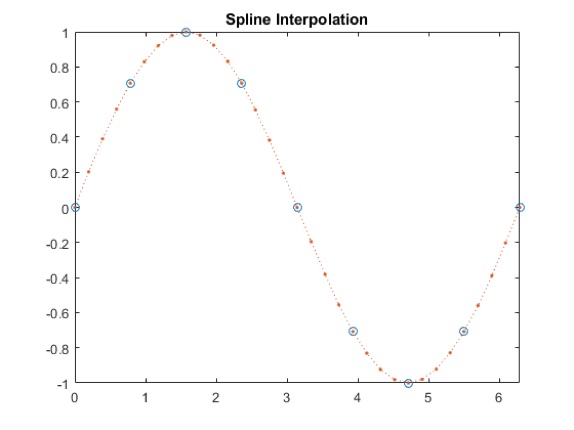
Beispielsweise funktioniert die Spline-Interpolation bei Schwingungs- und Geräuschaufnahmen recht gut, weil hierbei immer wiederkehrende Muster mit Sinus-ähnlicher Charakteristik auftreten.

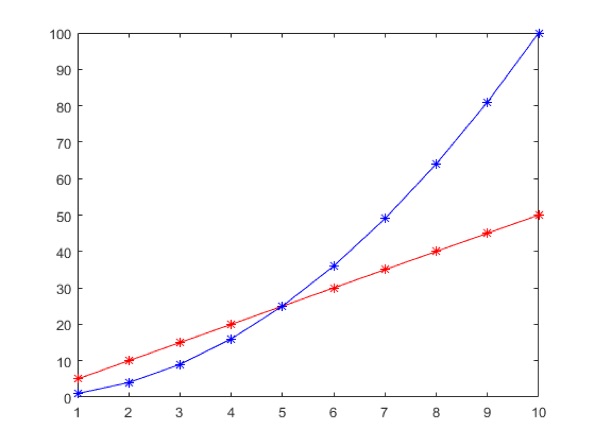
Wirklich schlechte Ergebnisse liefert hierbei eine Extrapolation.

x = 1:10;

v = (5*x)+(x.^2*1i);

xq = 1:0.25:10;

vq = interp1(x,v,xq);

figure

plot(x,real(v),'*r',xq,real(vq),'-r');

hold on

plot(x,imag(v),'*b',xq,imag(vq),'-b');

Details zu den entsprechenden Befehlen und Funktionen für 3D-Kennfelder

Vq = interp2(X,Y,V,Xq,Yq)

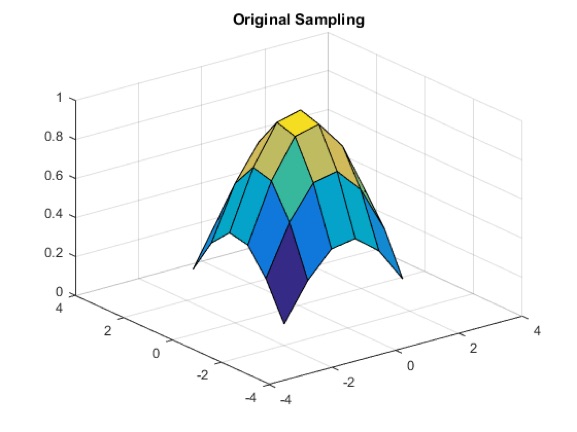
Das Funktionsprinzip lässt sich auch auf 3D-Kennfelder anwenden.

[X,Y] = meshgrid(-2:0.75:2);

R = sqrt(X.^2 + Y.^2)+ eps;

V = sin(R)./(R);

figure

surf(X,Y,V)

xlim([-4 4])

ylim([-4 4])

title('Original Sampling')

[Xq,Yq] = meshgrid(-3:0.2:3);

Vq = interp2(X,Y,V,Xq,Yq,'cubic',0);

figure

surf(Xq,Yq,Vq)

title('Cubic Interpolation with Vq=0 Outside Domain of X and Y');