Sonntag, 8. Juli 2012




Übertragungsfunktionen: Bode-Diagramm und Ortskurve zeichnen
Mit Matlab können mathematische Funktionen und Programme erstellt werden. Dabei seien hier weniger die analytischen Fähigkeiten, sondern das Rechnen mit Vektoren und Matrizen erwähnt. Aber auch Simulationen mit einem C-ähnlichen Programmcode können programmiert werden.
Bedienung:
Um mit Matlab loslegen zu können, sollte man sich bewusst machen, dass dies auf einer Kommandozeilen-Eingabe basiert. Also kann man die Befehle einzeln direkt in einem Eingabefenster eingeben und erhält sofort das Ergebnis. Je nachdem was der Befehl zum Ziel hat, kann man sich die Veränderung in einem anderen Fenster anzeigen lassen:
- Im "Command Window" kann man in einer Kommandozeile Befehle direkt eingeben und sieht dann dort das Ergebnis z.B. einer Berechnung. Wie beim Taschenrechner liegt das Ergebnis in der Speichervariablen "ans" vor und damit kann weitergearbeitet werden.
- Im "Workspace" liegen alle benutzten Speichervariablen bereit und es werden deren aktuellen Werte angezeigt. Dies können entweder skalare Werte sein, oder auch Vektoren und sogar Matrizen.
- In der "Command History" findet man die zuletzt verwendeten Befehle und kann diese mit einem Doppelklick erneut in das "Command Window" einfügen und dort ausführen lassen.
-
-Im "Current Directory" kann man sich ähnlich wie im Mac Finder/Windows Explorer in der Listenansicht durch die Ordnerstruktur auf der Festplatte hangeln und navigieren.
Natürlich kommt man über die einzelne Eingabe von Befehlen sehr schnell an Grenzen. Daher ist es möglich ganze Programme von Befehlen zu verfassen und diese als "M-Dateien" abzulegen. Diese M-Dateien lassen sich per Drag&Drop über das Programmfenster öffnen oder über das Fenster "Current Directory" dorthin navigieren. Diese Befehlsskripte stellen Matlab-Programme dar, welche sich auch gegenseitig aufrufen können. Wichtig ist, dass alle Dateien, die miteinander im Zugriff stehen, im selben Ordner liegen müssen.
Hier einige Beispiele aus der Regelungstechnik:
Zur Darstellung von Übertragungsfunktionen R(t) kommt üblicherweise die Darstellung im Bodediagramm zum Einsatz. Dieses besteht aus 2 Teildiagrammen, zum einen der Amplitude aufgetragen über der Frequenz, darunter die Phasenverschiebung. Mit dieser Darstellung können sehr schnell Regelstrecken analysiert und optimiert werden, die Stabilität kann aus der Phasenverschiebung abgelesen werden.
z=[1 2]; % Zählerpolynom 1*s + 2 als Zeilenvektor
n=[1 2 1]; % Nennerpolynom 1*s^2 + 2*s + 1 als Zeilenvektor
% Definition der Übertragungsfunktion
g1=tf(z,n); % g1 = (s+2)/(s^2+2*s+1)

Kurz zum Befehl "tf": damit kann eine Transferfunktion ausgeführt werden. Sprich: die Übertragungsfunktion R(t) wird als Koeffizienten-Matrix eingegeben. "z0" ist der Koeffizient des Zählerpolynoms, "n1" und "n2" sind die Koeffizienten des Nennerpolynoms.
step(g1); % Sprungantwort (Reaktion auf Einheitssprung) plotten
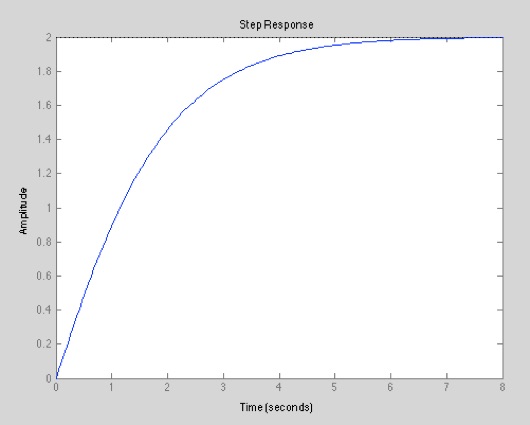
step(g1,10); % Sprungantwort von t=0 bis t=10
step(g1,0:0.01:10); % Sprungantwort von t=0 bis t=10 und alle 0.5s ein Rechenwert
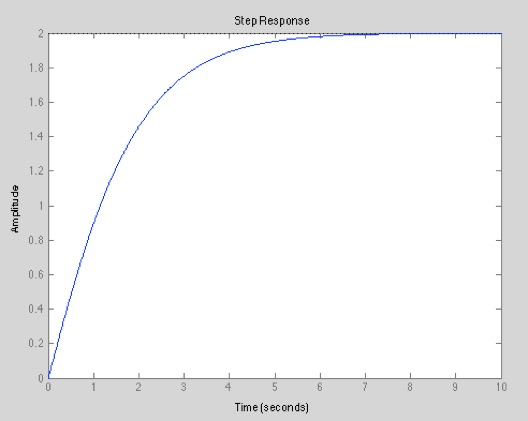
Besonders wichtig zu wissen ist, dass Matlab immer mit Vektoren arbeitet. Das heißt, dass man keine Variablen nur analytisch angeben kann und Matlab versteht diese, sondern eine Variable ist immer ein Vektor. Sprich: Wenn die Variable t verwendet werden soll, so wird diese über "t=-2:0.1:10" als ein Vektor definiert (hier startet t bei -2, das nächste Element wird um 0.1 erhöht bis als letztes der Vektor mit 10 beendet wird). Diese Vektoren und Matrixdenkweise ist anfangs immer ein großes Hindernis, da man eine solche Denkweise zuerst nicht gewohnt ist.
Klickt man jetzt auf die Variable t im "Workspace", dann kann der komplette Vektor angezeigt werden. Je kleiner die Zahl zwischen dem Start- und dem Endwert (hier 0.1) ist, desto feiner ist die Auflösung in der späteren Grafik. Ist dieser Wert z.B. 1, so sind die Treppensprünge in der grafischen Auswertung zu sehen.
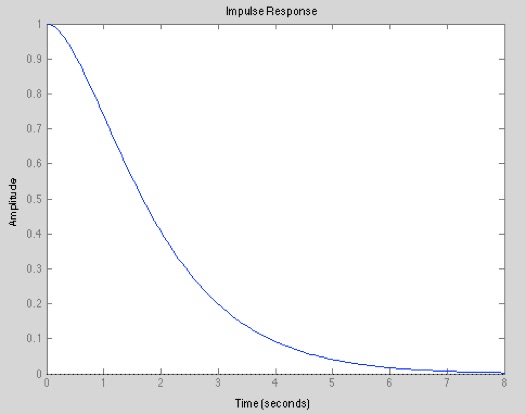
impulse(g1); % Stossantwort (Reaktion auf Dirac-Stoss)plotten
% weitere Varianten analog zu step(...)
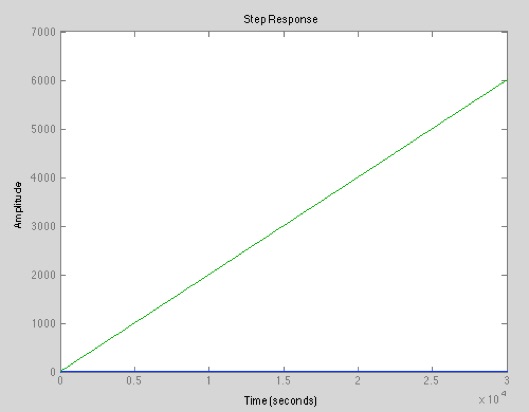
g2=tf([5 1],[5 0]); % g2 = (5s+1)/5s
step(g1,g2); % Sprungantwort von mehreren Übertragungsfunktionen
bode(g1); % Bodediagramm plotten
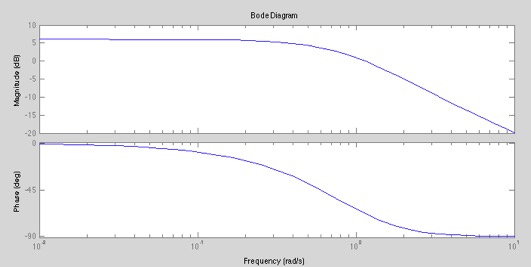
bode(g1,{1e-2,1e3}); % Bodediagramm von omega=0.01 bis 1000 plotten
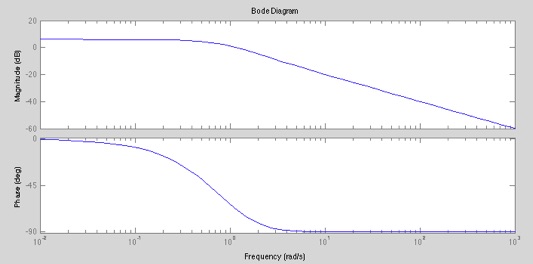
bode(g1,g2); % mehrere Bodediagramme aufeinmal
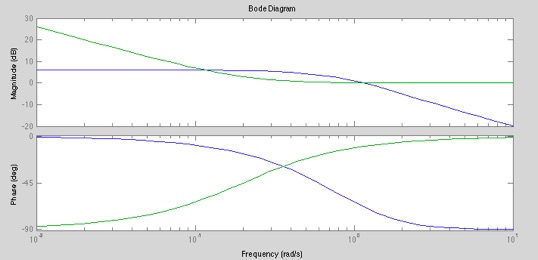
margin(g1); % Bodediagramm mit Phasen- und Amplitudenrand

f0=g2*g1; % Reihenschaltung von g1,g2 (z.B. Regler und Strecke)
fw=feedback(f0,1); % Rückkopplung (Gegenkopplung) mit
% f0 im Vorwärtszweig, 1 im Rückwärtszweig
% -> Führungsübertragungsfuktion
g2+g1; % Parallelschaltung von Übertragungsfunktionen
step(fw); % Sprungantwort des geschlossenen Regelkreises
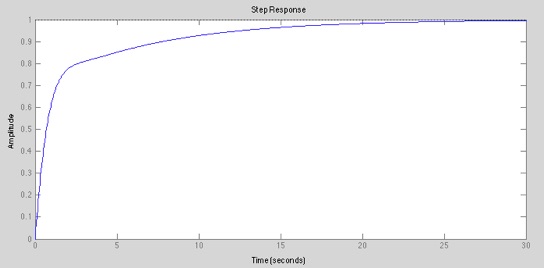
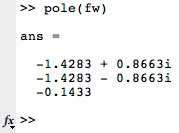
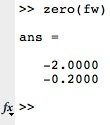
zero(fw); % berechnet die Nullstellen von Fw
dcgain(fw); % Verstärkung bei omega=0
% (Nullstellen,Polstellen und event.Vorfaktoren)um

g3=zpk([-1 -2],[-5,-3,-2],4);
% Definition einer Übertragungsfunktion in
% Pol-Nullstellenform mit Verstärkung

Der Befehl "bodeplot" zeichnet dann das Diagramm. Auch interessant ist die Darstellung als Ortskurve. Diese Funktionalität stellt Matlab ebenfalls bereit – in Form des Befehls
nyquist(g3);
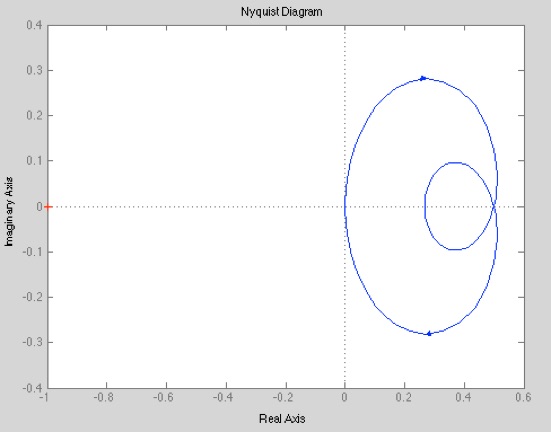
Das Nyquistdiagramm ist eine zweite Methode um Systeme zu analysieren. Im Gegensatz zum Bodediagramm wird beim Nyquistdiagramm Betrag und Phase in einem einzigen Diagramm dargestellt. Das macht das Nyquistdiagramm sehr übersichtlich. Mit dem Nyquistdiagramm wird es Ihnen später möglich sein, die Stabilität eines rückgekoppelten Systems auf einfache Weise zu bestimmen.
