Mit Hilfe von Matlab lassen sich beliebige Messsignale auf darin enthaltene Frequenzen untersuchen. Besonders interessant ist es zum Beispiel, die Eigenfrequenzen in einem aufgezeichneten Beschleunigungssignal herauszufiltern, um so die Anregung von bestimmten Resonanzfrequenzen festzustellen.

Hier ein Beispiel, in welchem eine 2-fache Sinusfunktion erzeugt und anschließend analysiert wird. Es werden die Frequenzen 8 Hz und 33 Hz erzeugt und anschließend über die Spektralanalyse wiederum dedektiert.

t = 0.01:0.01:0.5;                             % Zeitvektor (Fs = 100 Hz)
x = 5 + 8*sin(2*pi*8*t) + 4*cos(2*pi*33*t);    %Datenvektor ('Messwerte')

Ts = diff(t(1:2));                    % Abtastzeit
N = length(x);                        % Länge des Datenvektors
f=[0:floor((N-1)/2)] / (N*Ts);        % Frequenzvektor für Plot

X = fft(x);                           % Fouriertransformation
X = X / N;                            % Normierung
X = [X(1) 2*X(2:floor((N-1)/2)+1)];   % Begrenzen auf < F_max

figure
subplot (121)
    plot (t, x, '.-')
    title ('Signal')
    xlabel ('Zeit [s]')

subplot (122)
    stem(f, abs(X))
    xlabel ('Frequenz [Hz]')
    ylabel ('Amplitude')
    title ('Spektrum')

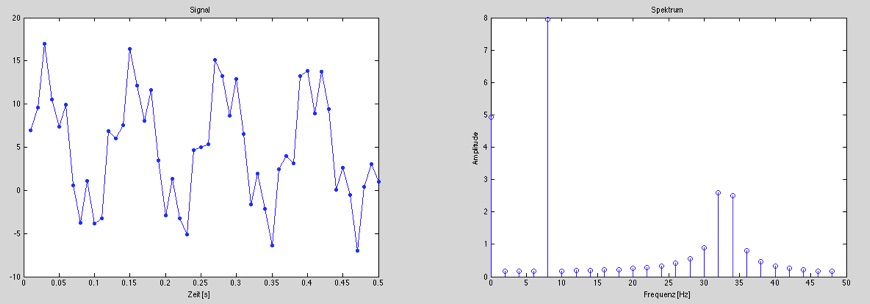
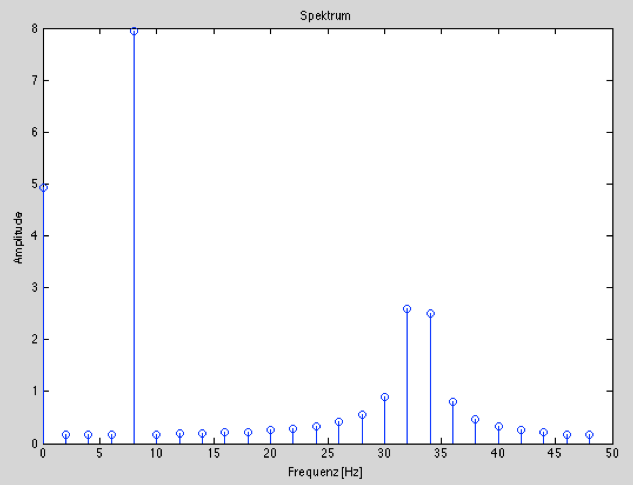
Wie man auf dem Frequenz-Diagramm sieht, wird die Frequenz 8 Hz genau getroffen und die korrekte Amplitude erkannt. Weniger genau wird die Frequenz 33 Hz getroffen, sondern die Frequenzunschärfe ist hier größer. Diese Unschärfe wird auch als Leakage-Effekt bezeichnet, dabei verteilt sich die Amplitude auch auf die Nachbarfrequenzen. Dies ist immer dann der Fall, wenn die gesamte Messzeit NTS kein ganzzahliges Vielfaches der Periodendauer der zu analysierenden Frequenz ist.

Um diese Unschärfe zu reduzieren gibt es mehrere Möglichkeiten. Am naheliegendsten wäre es, die Frequenzauflösung ∆F zu verfeinern. Dies hat aber auch ein stärkeres Rauschen zur Folge. Eine bessere Möglichkeit ist die Verwendung von Fensterfunktionen. Zusätzlich bietet sich eine Mittelwertbildung (Averaging) im Frequenzbereich an.

Averaging

Hierbei wird ein langer Messdatensatz in definiert lange Teilbereiche untergliedert, diese einer Spektralanalyse unterzogen und die Ergebnisse miteinander gemittelt. Das Rauschen wird dadurch auf ein gleichmäßiges Niveau egalisiert.

Fensterung

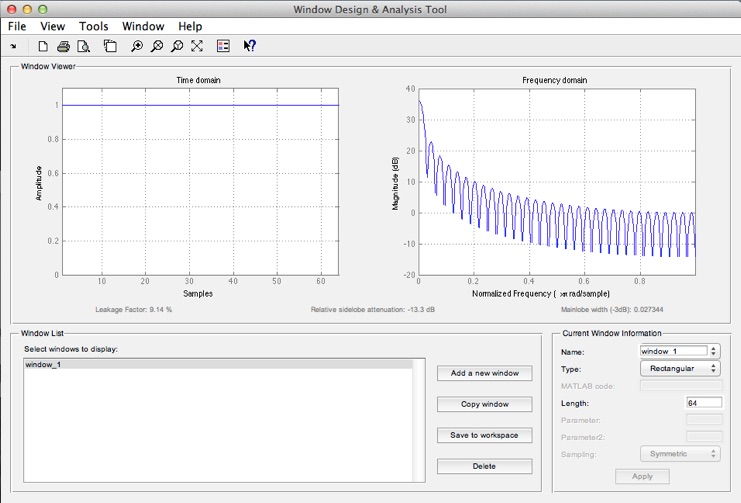
ZurVerminderung des Leakage-Effekts kann eine Fensterung vor der diskreten Fouriertransformation durchgeführt werden. Dabei wird aus der langen Messreihe ein Teilbereich „gefenstert“, also herausgeschnitten. Wird dieser Ausschnitt direkt verwendet und analysiert, so wird dies als Rechteck-Fensterfunktion bezeichnet. Es gibt aber auch eine mehr oder weniger scharfkantige Ausblendung am Rand des Fensters. Hierzu nachfolgend einige Filtertypen für Fensterung. Zur Einarbeitung in die Fensterung gibt es  in Matlab den Befehl

wintool

rectwin(länge);    % Rechteck

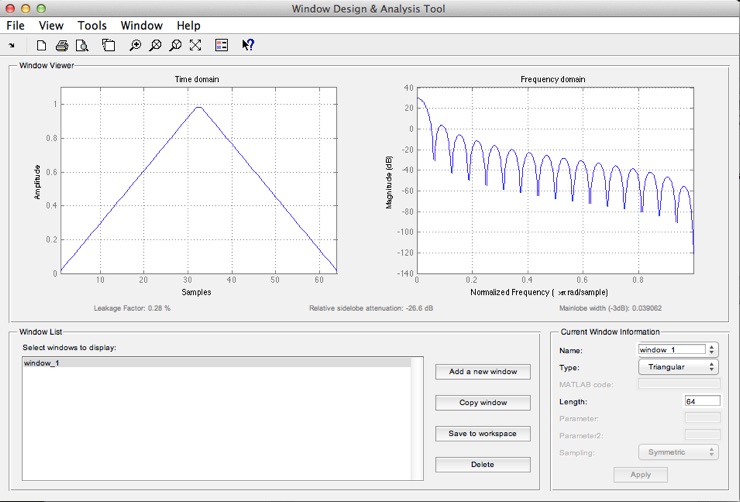
triang(länge);    % Dreieck (Rand > 0)

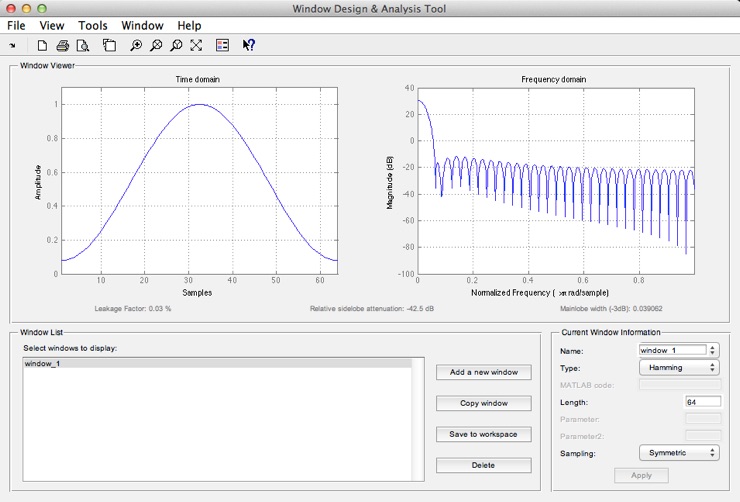
hamming(länge);    % Hamming

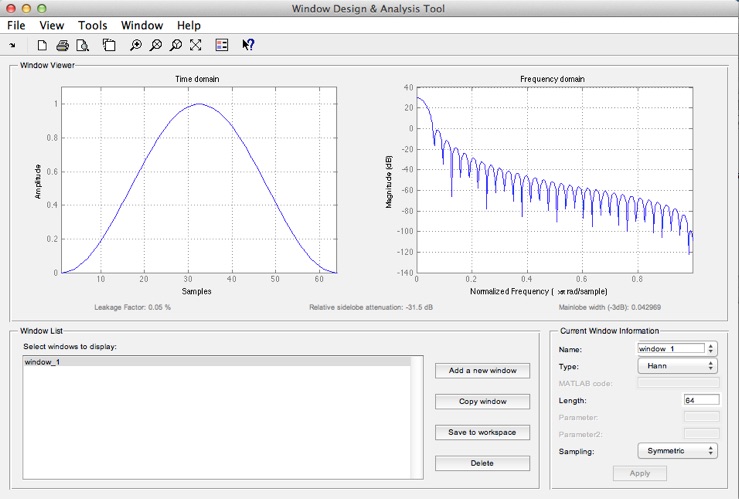
hann(länge);    % Hann

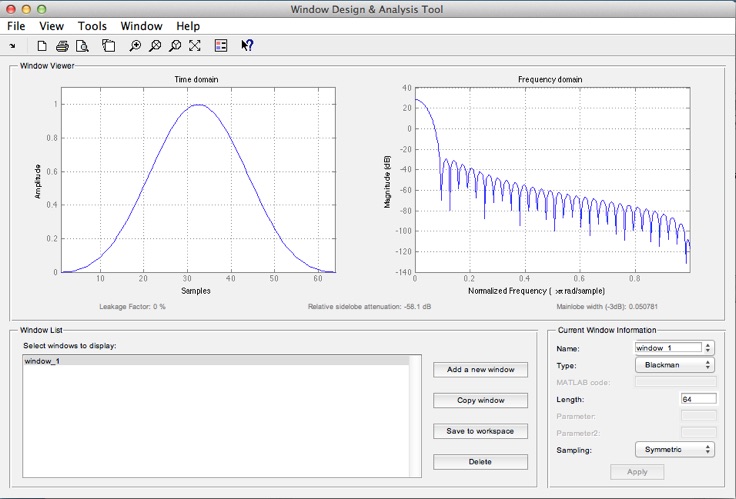
blackman(länge);    % Blackman

Leistungsspektren

Alternativ zur oben beschriebenen Amplitudenspektren werden häufig auch Leistungsspektren zur Analyse verwendet. Hierbei wird die in einem Messsignal enthaltene Leistung den einzelnen Frequenzen zugeteilt.

Über den Befehl pwelch wird das Autoleistungsdichtespektrum erzeugt.

t = 0.01:0.01:25;                             % Zeitvektor (Fs = 100 Hz)
x = 2 + 8*sin(2*pi*8*t) + 4*cos(2*pi*33*t);   % Datenvektor ("Messwerte")
x = x + 5*(randn (1,length(t)));              % Rauschen hinzufügen

[Pxx, F] = pwelch (x, rectwin (250), [], 250, 100);
plot (F, 10*log10(Pxx))

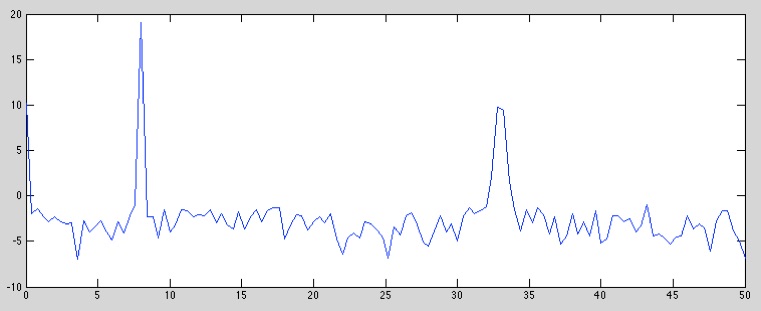
Eine weitere Möglichkeit zur interaktiven Analyse bietet der „Spektrum Viewer“, welcher mittels des Befehls sptool aufgerufen wird. Im sich jetzt öffnenden Fenster sollte über den Menübefehl „File/Import“ ein Messsignal ausgewählt und die Abtastfrequenz eingegeben werden.

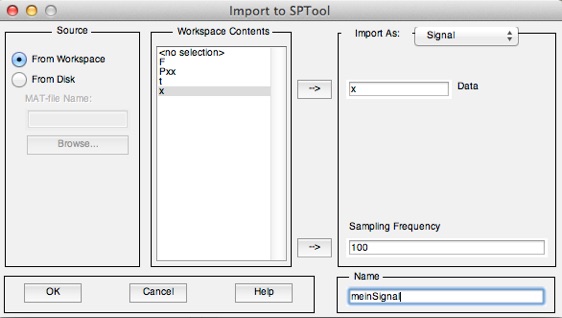
Anschließend steht das Messsignal bereit und kann über den Knopf „View“ ausgewertet werden.

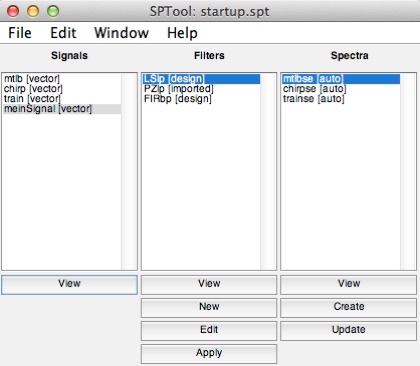
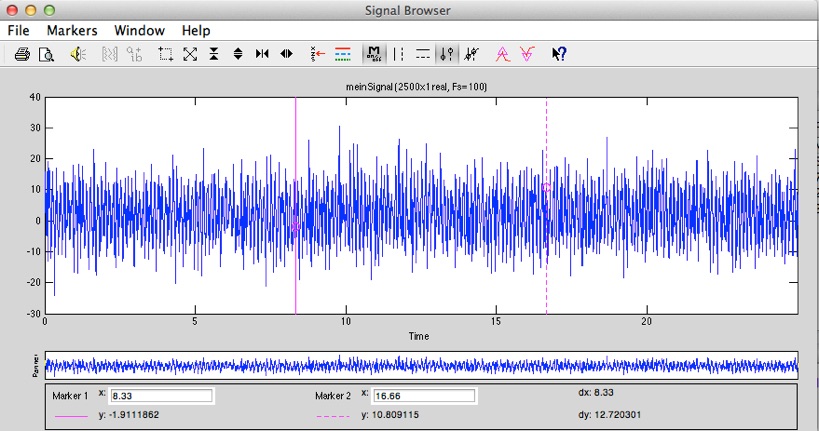
Mit dem Befehl cspd(x, y, fenster, ueberlappung, Nfft, Fs) kann man das Kreuzleistungsspektrum der Signale x und y bestimmen.

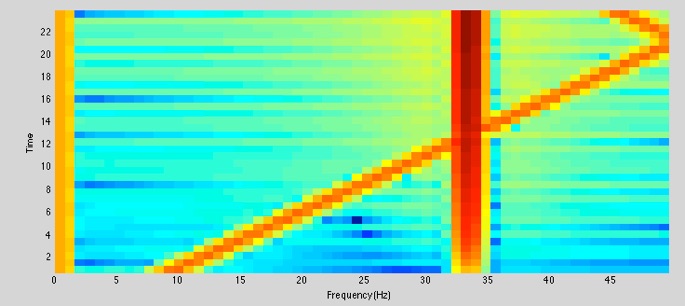
Um nichtperiodische Signal wie z.B. Geräusche oder Sprachsignale zu analysieren gibt es den Befehl spectrogram. Dabei können Komponenten aus Messsignalen herausanalyiert werden, welche ihre Frequenz und Amplitude über der Zeit ändern.

t = 0.01:0.01:25;                                        % Zeitvektor (Fs = 100 Hz)
x = 2 + 8*sin(2*pi*(8+t).*t) + 4.*t.*cos(2*pi*33.*t);    % Datenvektor mit frequenzvariablem
                                                           und amplitudenvariablem Anteil
spectrogram(x, 125, [], 125, 100)                        % Spektralanalyse mit spectrogram